FW: [xmca] a minus times a plus

["Au, Wayne" <wau@Exchange.FULLERTON.EDU>]

From: Wayne Au <wau@exchange.fullerton.edu>
Date: Thu, 30 Apr 2009 19:48:57 -0700
To: "eXtended Mind, Culture, Activity ," <mcole@weber.ucsd.eduxmca@weber.ucsd.edu>, "eXtended Mind, Culture, Activity" <xmca@weber.ucsd.edu>
Conversation: [xmca] a minus times a plus
Subject: Re: [xmca] a minus times a plus

Mike,
For what it is worth, I posed this question to my father, a physicist by training, and retired math instructor. I don’t know that I totally follow it, but I found it interesting nonetheless. His answer, which comes from some work he did with public school math teachers (trying to get them to better understand foundational mathematics), follows. By the way, my father very much agrees with Liping Ma’s work with elementary math teachers (recently mentioned on this string).

- Wayne


Why is the negative of a negative positive? Six Explanations
There are many ways to answer this question, depending on what is intended to be accomplished. Several ways turn out to be psychologically useful, in the sense that students tend to feel at ease when they see one or more of these answers. Some of “pictoral” or “geometric” while others are “algebraic.”

1.     Historical: Negative numbers first arose in China & India because of the emergence of well-devel­oped mercantile societies. Merchants quickly arrived at the idea that debt & credit were very useful in order to facilitate trade & this gave rise to numbers being written in red & black ink. To this day, we refer to debts as “red ink” items & credits as “black ink” items.[1] <#_ftn1>

A merchant might have reasoned as follows: If I have no debt, how can I subtract a debt of 5 yuan? Simple! Let me borrow 5 yuan from the moneylender so now I have 5 yuan & a debt of 5 yuan. If I subtract this debt of 5 yuan, I am left with 5 yuan. Thus the subtraction of a debt of 5 yuan is equivalent to being given 5 yuan.

2.     Formal. What is going on in the “merchant explanation” is easy to understand in modern notation:
–(–5) =  0 – (–5),
= 5 + (–5) – (–5)
= 5 + 0 = 5.
Replacing 5 by any number a, we see that the argument just given is valid in general:
–(– a) = 0 – (–a),                      For any number x, 0 + x = x.
= a + (–a) – (–a)             a + (–a) = 0, by definition.
= a + 0                             (–a) – (–a) = 0.
= a.

3.     Psychological (Algebraic) Note that

3(–5) = –15,
2(–5) = –10,
1(–5) = –5,
0(–5) = 0.

In going from one line down to the next, we had to increase the right side by +5. If this pattern is preserved, then.

–1(–5) = –(–5) = 5.

Replacing 5 by any number a gives

3(–a) = –3a,
2(–a) = –2a,
1(–a) = –a,
0(–a) = 0,

                                                        –1(–a) = –(–a) = a.
This explanation is “psychological” because it is designed to make us feel mentally at ease with the conclusion. It is a plausible explanation—the formal explanation is “rigorous”.

4.     Psychological (Geometric) Imagine the number line & interpret the minus sign as an instruction to “reflect” a number about 0; i.e., –5 means reflect the number 5 about 0 to give –5. Then the reflection of –5, –(–5), is 5. This viewpoint, applied to any number a, gives –(–a) = a. Again, this is a plausible explanation, designed to make us feel comfortable with the results.

5.     Psychological (Graphical) Graph y = –x, beginning with only positive values or 0 for x. We have points such as (0, 0), (1, –1), (2, –2), (3, –3), etc. If these points are graphed & a line drawn through them, it slants from the origin into the 4th quadrant—the solid part of the line in the figure. If the solid line is extended into the region where x is negative, it enters the 2nd quadrant where the values of y are positive; i.e., if x is any negative number, say, x = –a, where a > 0, then y = –x =  –(–a) =  a is positive.

6.     Multiplication Involving Negative Numbers, Considered Formally. The usual rules for products of positive numbers & negative numbers follow directly from the most basic property that negative numbers satisfy:

b + (–b) = 0.

Multiplying both sides of the equation by a, we have


ab + a(–b) = 0,
[cid:3323965926_964290]

If, for the moment, we take a & b to be positive numbers, then commutativity of positive numbers says that
ba = ab,
so with b + (–b) = 0, we have
ba + (–b)a = 0,
ab + (–b)a = 0,



This immediately gives  (–b)a = –ab = a(–b)

(–a)b + (–a)(–b) = 0,



  –ab + (–a)(–b) = 0,
  (–a)(–b) = ab.


[1] <#_ftnref1>    “For subtraction—with the same signs tale away one from the other; with different signs add one to the other; positive taken from nothing makes negative, negative from nothing makes positive.” This is from a German translation (Neun Bücher arithmeticsher Technik by Kurt Vogel) of the Chinese text, jiuzhang suanshu (variously translated as Nine Chapters of the Mathematical Arts or Arithmetic in Nine Sections, circa 100 b.c.?)



On 4/27/09 3:47 PM, "Mike Cole" <lchcmike@gmail.com> wrote:

Since we have some mathematically literate folks on xmca, could someone
please post an explanation of why

multiplying a negative number by a positive numbers yields a negative
number? What I would really love is an explanation
that is representable in a manner understandable to old college professors
and young high school students alike.

mike
_______________________________________________
xmca mailing list
xmca@weber.ucsd.edu
http://dss.ucsd.edu/mailman/listinfo/xmca



--
Wayne Au
Assistant Professor
Department of Secondary Education
CSU Fullerton
P.O. Box 6868
Fullerton, CA 92834
Office: 714.278.5481
Editorial Board Member: Rethinking Schools (www.rethinkingschools.org)
http://ed.fullerton.edu/SecEd/Faculty/Full_Time_Faculty/Au.html

“Education must keep broad ideals before it, and never forget that it is dealing with Souls and not with Dollars.” - W.E.B. DuBois

------ End of Forwarded Message

_______________________________________________
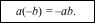
xmca mailing list
xmca@weber.ucsd.edu
http://dss.ucsd.edu/mailman/listinfo/xmca